|
| |
|
When a sound wave travels down a tube filled with air, some of the sound wave will reflect back when it gets to the end of the tube, whether the tube end is open or closed. Sound waves will reflect back and forth from one end to the other. Certain specific vibrational frequencies will form standing waves in the air column, and these are the frequencies at which the column of air will resonate. Many musical instruments use standing waves in air columns as the initial source of their sound waves. Brass and woodwind instruments use air columns to produce their characteristic sounds. When a standing wave forms in an air column, there is always a displacement antinode at any open end and a displacement node at any closed end. Note: Displacement nodes and antinodes are points that undergo minimum and maximum displacements respectively. In terms of pressure, they are actually the opposite. Displacement nodes are pressure antinodes and displacement antinodes are pressure nodes. This can be seen in the longitudinal waves in the animations - notice how the areas where there are stationary lines (displacement nodes) have large variations in line density (pressure antinodes). On this site, when the word node or antinode is used alone, it refers to a displacement node or antinode. If the air column is open at both ends, the fundamental mode of vibration has a single node at the center and an antinode at each end. This is also known as the first harmonic. For the first harmonic, the length of the air column is equal to one half of a wavelength of the standing wave, because the distance from one antinode to the next nearest antinode is one half a wavelength. The frequency of the first harmonic is known as the fundamental frequency (f0) In the diagrams below, the standing wave is shown in both its longitudinal and transverse forms. The actual sound wave is longitudinal, but the nodes and antinodes are easier to visualize in the form of the equivalent transverse wave. | |
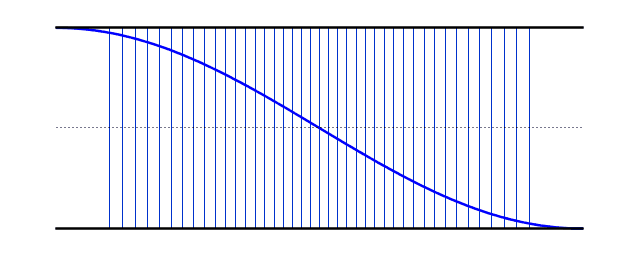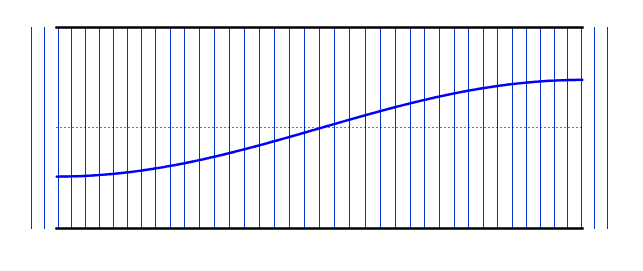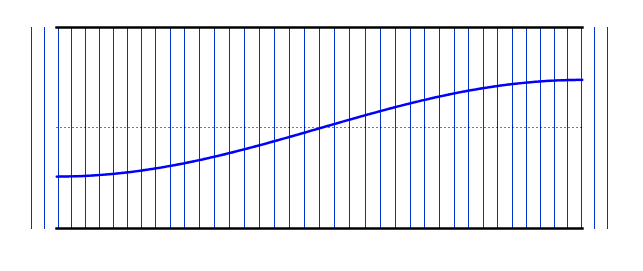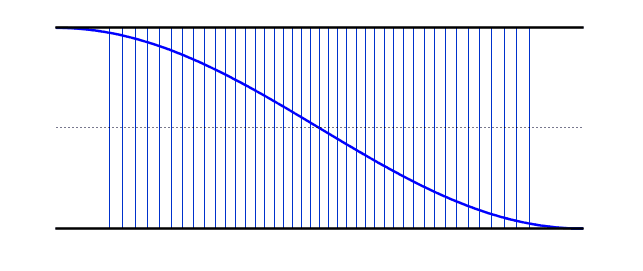 Fundamental Frequency (First Harmonic) |
f = f0 L = λ/2 λ = 2L |
| At the 2nd harmonic the wavelength is half the wavelength of the fundamental and therefore the frequency is twice that of the fundamental. | |
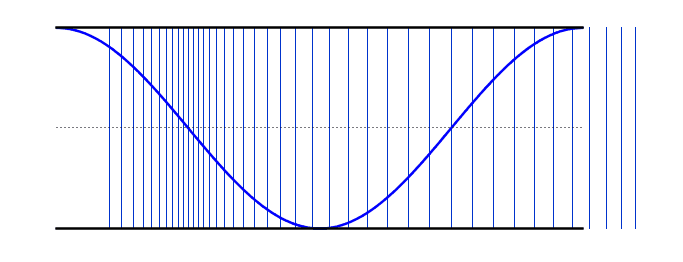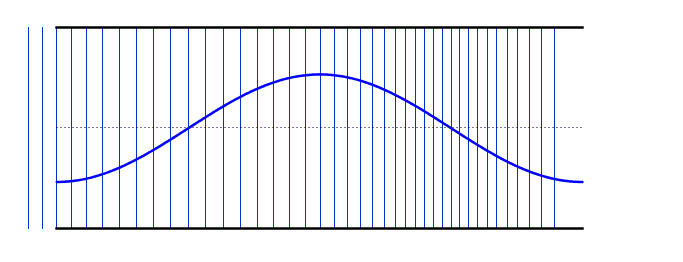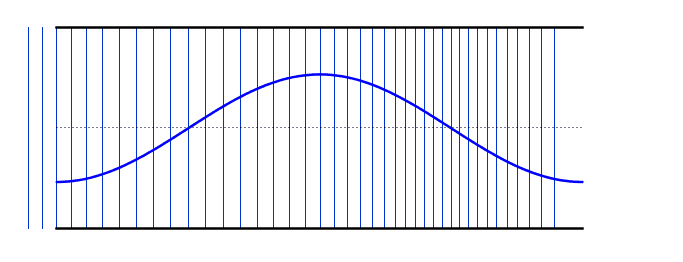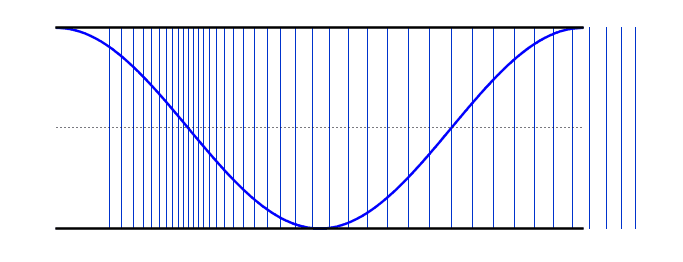 2nd Harmonic |
f = 2f0 L = λ λ = L |
| At the 3rd harmonic the wavelength is one third the wavelength of the fundamental and therefore the frequency is three times that of the fundamental. | |
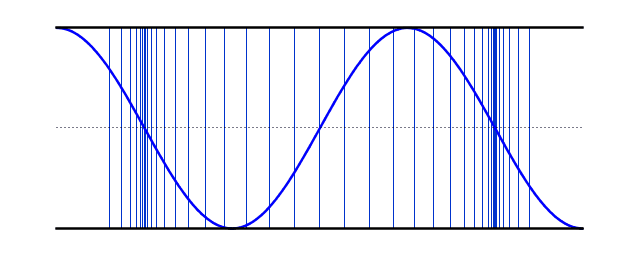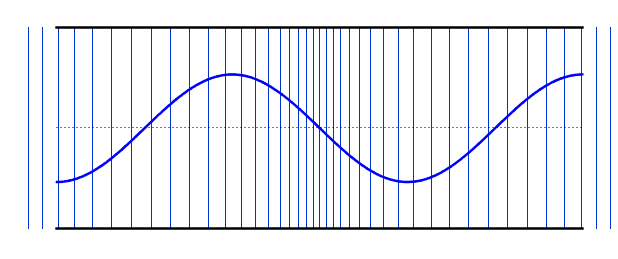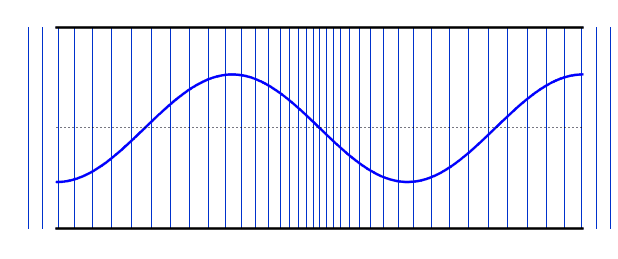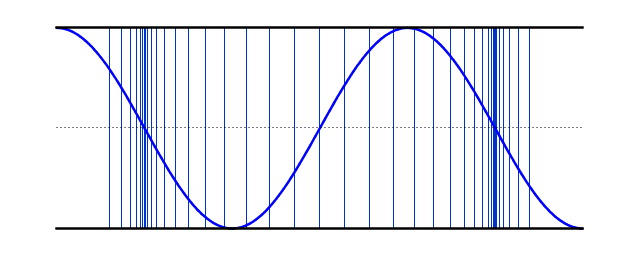 3rd Harmonic |
f = 3f0 L = 3λ/2 λ = 2L/3 |